Table of Contents
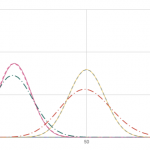
2項分布 (textrm{Binomial}(m, p)) は 正規分布、 ポアソン分布 に近い分布になります。
特に (n) が大きければ、 中心極限定理から、 正規分布で近似できるということを理論的に知っている人もいるでしょう。
これらの3つの分布のグラフを表示して確認してみましょう。
グラフ表示の基本
グラフ表示は Google Spreadsheet で行いました。 Google Spreadsheet では、 2項分布は BINOMDIST, 正規分布は NORMDIST, ポアソン分布は POISSON.DIST で計算できます。
(n=100)
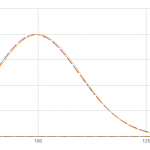
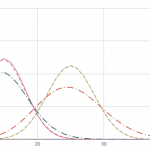
2項分布で ( n = 100 ) の場合の近似を比較してみます。 正規分布は (textrm{Normal}(np, sqrt{np(1-p)})) , ポアソン分布は (textrm{Poisson}(np)) を比較します。
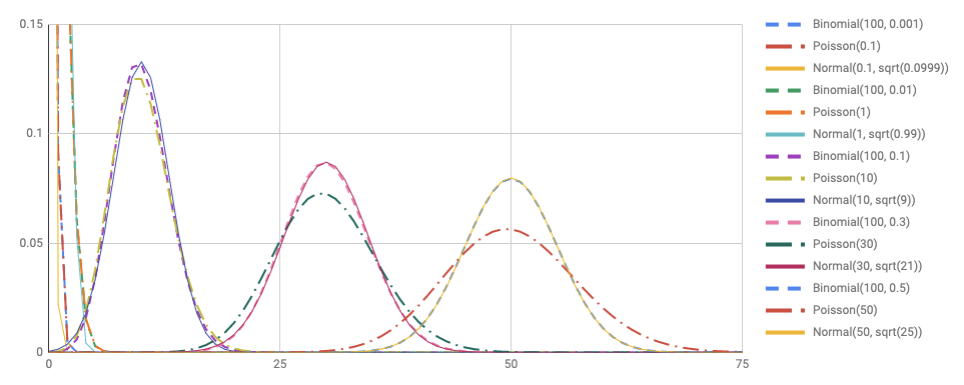
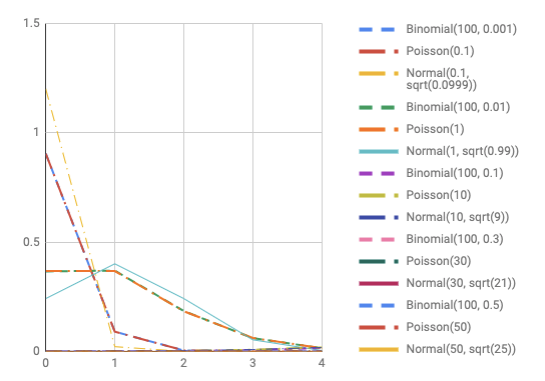
(p) の値をいろいろと変えてグラフを表示しています。 右の山から順に (p = 0.5), (p = 0.3), (p = 0.1) です。 さらにその左に表示されているのは ( p = 0.001, 0.0001 ) のグラフです。
( p = 0.5, 0.3, 0.1 ) は2項分布と正規分布がものすごくよく似た値になっていますね。
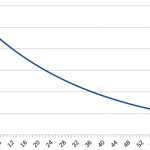
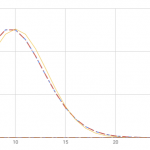
(p=0.001, 0.0001) の グラフを表示するエリアを変えて確認してみます。
正規分布よりもポアソン分布のほうが2項分布に近くなっているのがわかるでしょうか。 基本的に (p) がとても小さい場合、 正規分布では全ての確率を足した時に1になるようにするために、 (x = np) のときの確率が1より高くする必要が出てきます。 1より高いと確率の関数として成り立ちませんから、 (p) があまりにも小さい場合は正規分布は2項分布からずれてきます。
(n=1000)
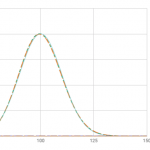
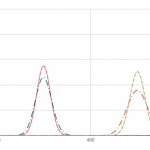
(n = 1000) の場合のグラフは次のようになります。
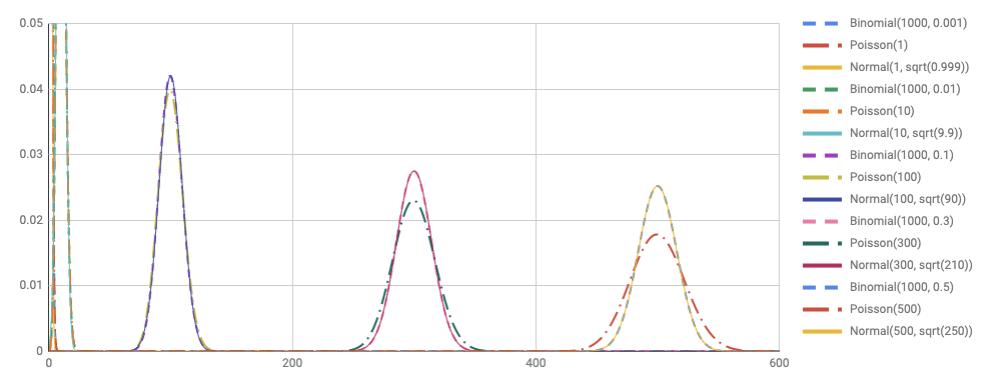
これも右から (p = 0.5), (p = 0.3), (p = 0.1) のグラフとなっています。 2項分布と正規分布はまさに瓜二つですね。 ポアソン分布は確実にずれていることがわかります。
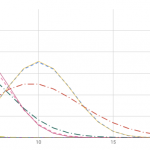
(p= 0.001, 0.0001) のグラフを表示します。
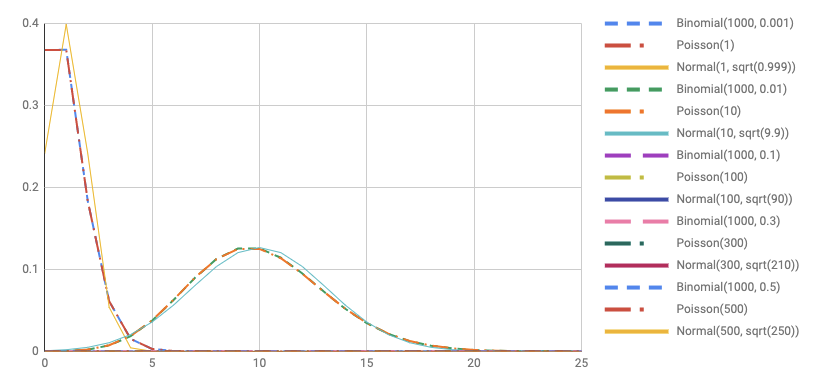
正規分布もポアソン分布もどちらも似ていますが、 どちらかというとポアソン分布のほうが2項分布に近いですね。
(n=10000)
(p=0.01) 以上 の場合は2項分布と正規分布がそっくりになることがわかりました。 (n=10000, p = 0.001 ) の場合のグラフを比較してみます。
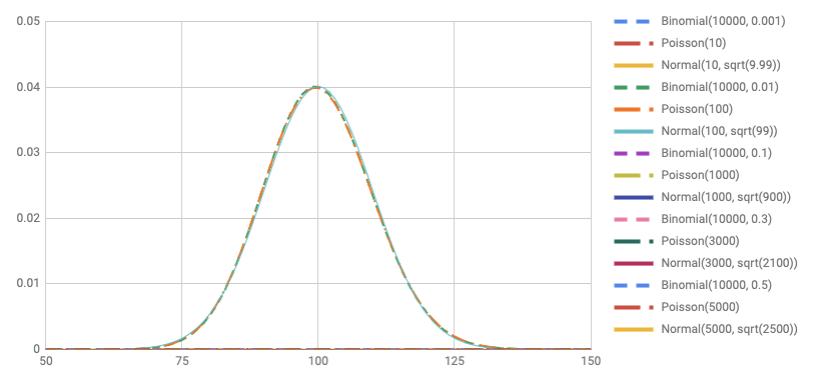
ここまでくると正規分布でもわずかな差になっていますが、やはりポアソン分布のほうが2項分布に似ていますね。 似ているというよりそっくりです。
(p=0.0001) の場合も見てみます。
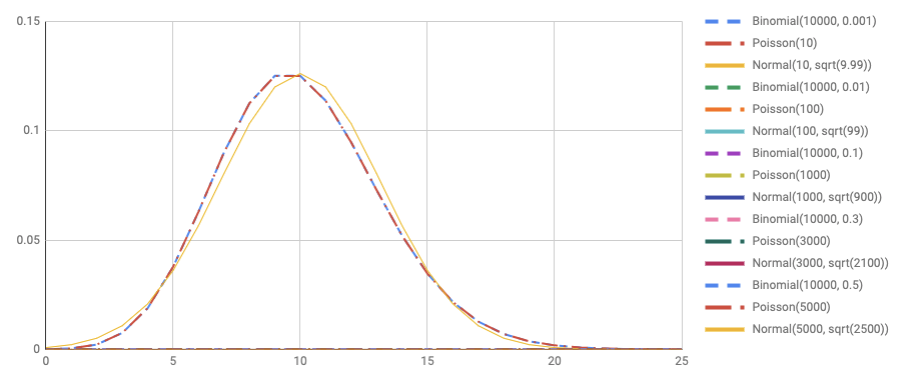
こちらも正規分布が似てきていますが、ポアソン分布のほうが2項分布に近いですね。
(n=100000)
(p=0.0001) でも (n=100000) だったら正規分布も2項分布にそっくりになるかもしれません。 比較してみましょう。
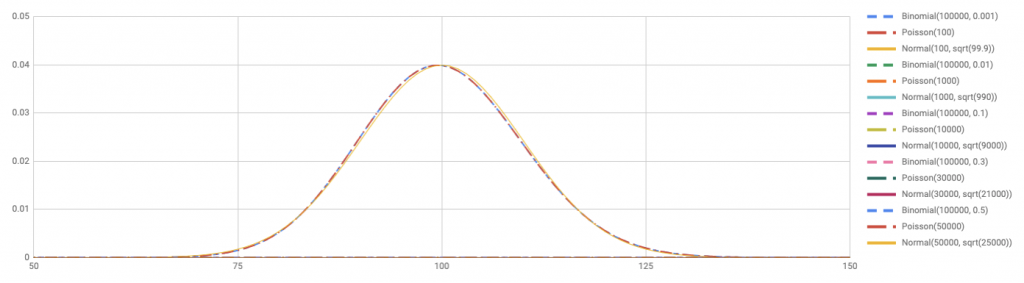
実際には正規分布を使ってもいいのかもしれませんが、ポアソン分布のほうが2項分布に近いです。 (n) を大きくして比較してきましたが、(p)が小さければポアソン分布のほうが2項分布に近いんですね。
(n=50)
(p geq 0.01) では 2項分布に近いように見えた正規分布ですが、 (n) を小さくしても2項分布に近い値を出すのでしょうか。 (n=50) で比較してみます。
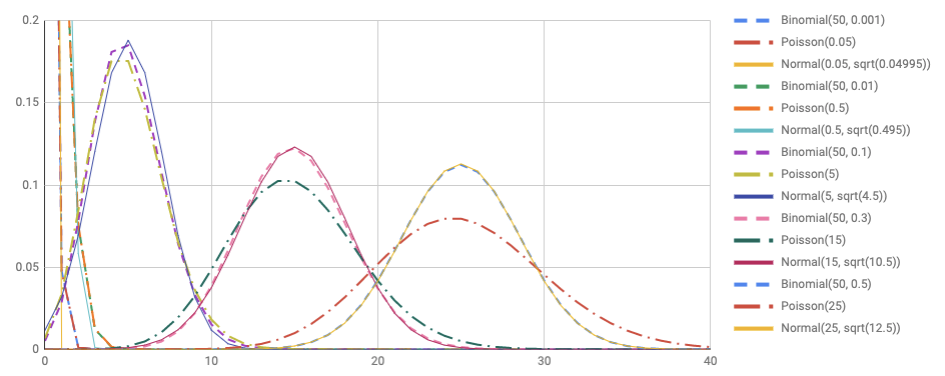
(n=100) の時に比べれば 2項分布と正規分布の差は開いていますが、 まだまだだいぶ似ている感じがします。
(n=20)
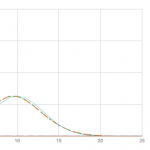
(n=20) の場合にも見てみましょう。
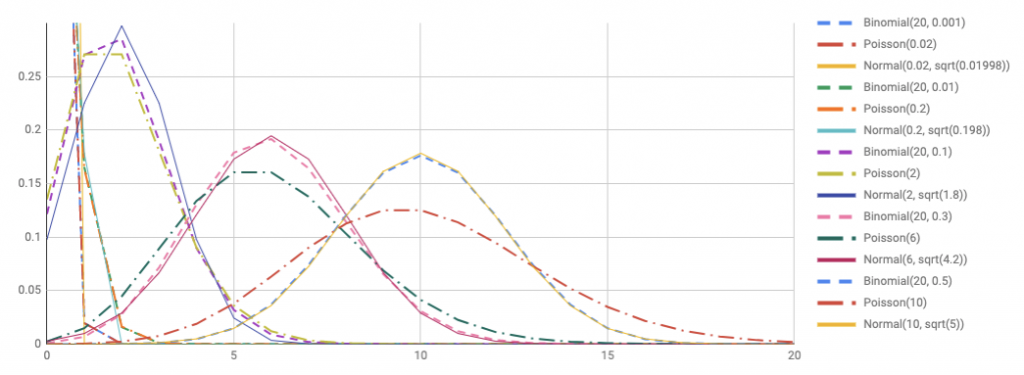
(p=0.1) のグラフはズレが大きいですね。 (p geq 0.03) ではまだ近似として正規分布が使えそうです。
(n=10)
(n=10) の場合も見てみましょう。
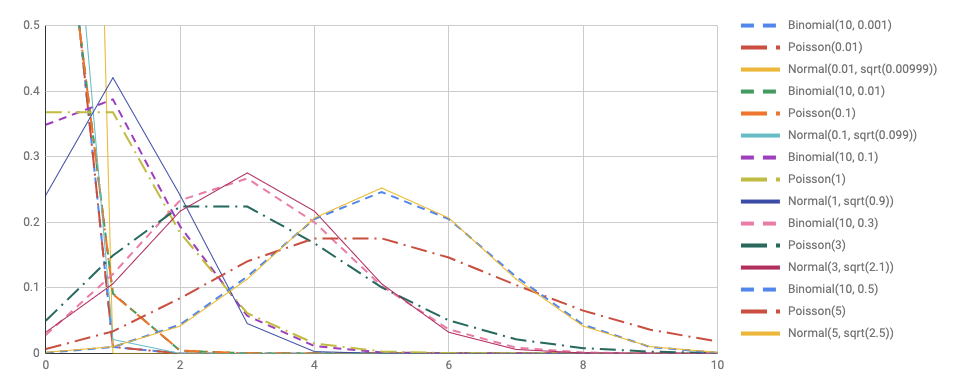
(p=0.03) のところもズレが大きくなり始めましたが、 (n=10) でも (p) の値によっては近似として使えそうな印象です。
以上、正規分布、ポアソン分布、2項分布の差を視覚的に表示しました。 特に、 (p) が小さい場合は正規分布よりもポアソン分布のほうが2項分布に近くなることが視覚的にわかりましたね。