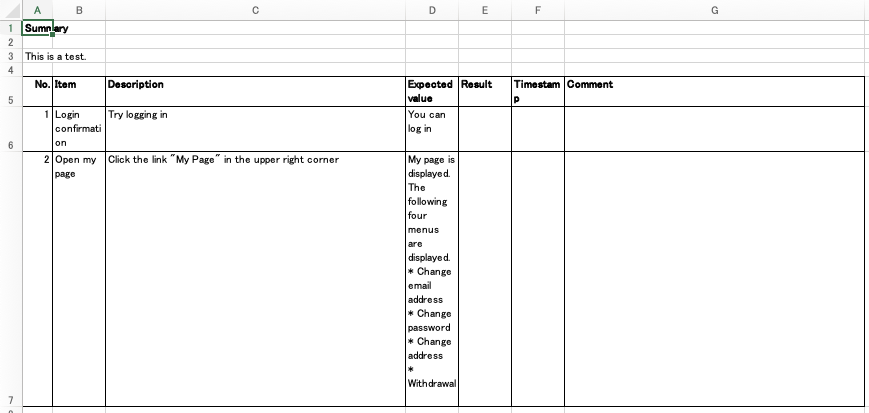
Table of Contents
Irrational numbers ( a ) , ( b ) exist that make ( a^b ) rational.
Prove with law of excluded middle and without fixing what ( a ) and ( b ) are.
Proof
Supporse ( x = sqrt{2} ^ sqrt{2} ) .
Case: ( x ) is Rational
( sqrt{2} ) is irrational, so ( a = b = sqrt{2} ) make ( a^b ) rational. ( ( sqrt{2} ) が無理数であることの証明は 証明: ( sqrt{2} ) は無理数 をご覧ください。)
Case: ( x ) is Irrational
begin{eqnarray*} sqrt{2} & = & (sqrt{2}^sqrt{2})^sqrt{2} & = & sqrt{2}^{sqrt{2} cdot sqrt{2}} & = & sqrt{2}^2 & = & 2 end{eqnarray*}Then, ( a = x = sqrt{2}^sqrt{2} ) and ( b = sqrt{2} ) are irrational and make ( a^b ) rational.
Above all, there are irrational numbers ( a ) and ( b ) that make ( a^b ) rational.