アルゴリズムの評価

いいアルゴリズムとはどのようなアルゴリズムでしょうか。アルゴリズムの良し悪しを決める基準のことをアルゴリズムの評価基準といいます。ここではそのアルゴリズムの評価基準について考えてみましょう。

計算量

一般に、アルゴリズムの評価は計算量によって行われます。計算量には、つぎのものがあります。

時間計算量 (time complexity)

アルゴリズムの実行時間を表します。早ければ早いほど良いです。

最良時間計算量 (best time complexity): 最も速くアルゴリズムを実行できる場合の時間計算量です。配列のソートの処理において、ソート対象の配列が既にソートされている場合などが該当します。
最悪時間計算量 (worst time complexity): アルゴリズムの実行に最も時間のかかる場合の計算量です。探索アルゴリズムですべてのノードを探索する必要がある場合などが該当します。アルゴリズムによって最悪の入力データは異なってくるので、アルゴリズムごとにデータの検討が必要です。
平均時間計算量 (average time complexity): 入力にある分布を仮定してすべての入力に対する時間計算量の期待値を計算したものです。多くの場合、最悪時間計算量とほぼ同じになります。

領域計算量 (space complexity)

アルゴリズムのデータ使用量を表します。小さければ小さいほど良いです。時間計算量の大きいものは領域計算量も大きくなり、また逆に、領域計算量が大きいものは時間計算量も大きくなる傾向が強いです。

よく使われるのは時間計算量です。ただし、時間計算量を正確に計算することは難しいため、コードの命令がどれだけ実行されるのかを計算して、目安の指標を考えます。

注意点

平均時間計算量は、すべての入力可能なデータとその出現確率を決定して計算する必要があるので簡単には計算できません。多くはどのデータも均等に出現すると仮定して計算しますが、そういう仮定をすると実際の実行環境にそぐわないこともあります。

しかし、同じことは最悪時間計算量についてもいえます。最悪のデータが滅多に出現しない環境で、最悪の場合ばかりを心配しても実践的ではありません。そのため、最悪時間計算量も平均時間計算量も使われています。

計算量の漸近的評価

計算量の評価は、入力サイズ ( n ) の値が非常に大きい場合を想定して行われます。そのときの計算量を 漸近的な時間計算量 といいます。 (入力サイズの値が小さい場合はアルゴリズムを比較しても大きな差は生まれません。)

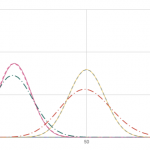
たとえば、ここに入力サイズが ( n ) である問題に対して全く同じ動作をするアルゴリズム A, B, C があり、それぞれの時間計算量が次のようになっていたとします。

begin{array}{ccl} textrm{A} & : & 10 n ^2 + 90 n + 400 textrm{B} & : & n ^ 4 – n ^ 3 – n textrm{C} & : & 100n ^ 3 end{array}

この3つのアルゴリズムを、 ( n ) が限りなく大きくなったときの時間計算量が小さい順に並べると A, C, B となります。

オーダ記法 (O notation)

漸近的な時間計算量を表すのに オーダ記法 が用いられます。オーダ記法は次のように定義されます。

入力サイズ ( n ) の関数として定義される時間計算量 ( T(n) ) が、ある関数 ( f(n) ) に対して ( O(f(n)) ) であるとは、適当な2つの正の定数 ( n_0 ) と ( c ) が存在し、 ( n_0 ) 以上のすべての ( n ) について ( T(n) leq c f(n) ) が成り立つことをいう。

記号を使って書くと次のようになります。

[ T(n) = O(f(n)) Leftrightarrow exists n_0, c ; forall n geq n_0 , ; T(n) leq c f(n) ]

計算量のオーダによって、入力サイズ ( n ) の変化が大きく影響するため、オーダ記法で考える習慣があります。

それでは先ほどの A, B, C のアルゴリズムの実行時間のオーダ記法を考えてみます。

A の時間計算量は ( 10 n ^ 2 + 90 n + 400 ) でした。この中で最も増分の大きい主要項は ( 10 n^2 ) です。よって、オーダ記法では ( O(n^2) ) と書けます。

注意点

オーダの優劣だけでアルゴリズムの実行時間を評価するのは危険です。

オーダ記法では一番影響の大きい主要項を基準に考えます。そのため ( 100 n ) も ( 0.5 n ) も ( O (n) ) となります。また、 ( 30 n ^ 2 + 20 n ) と ( n ^ 3 + 4 n ) では ( n leq 30 ) のときは前者のほうが速くなります。

オーダの優劣

( n ) が大きいとき、次の不等式が成り立つ。

[ log n lt sqrt{n} lt n lt n log n lt n ^ 2 lt n ^ 3 lt cdots lt 2 ^ n lt n! ]

また、オーダが ( n ) によって変わらない、定数である場合は ( O(1) ) と記述する。

例

時間計算量の計算例です。次のように、配列で ( n ) 個の整数が渡された場合に、同じ数があれば出力するアルゴリズムを考えます。

<?php
/* $numbers is an array of number
*
* == Example
* $numbers = array(1,2,3,4,5,6,1,2,3,4,5,6,7,2,7,3);
*/
$secondSup = count($numbers);
$firstSup  = $secondSup - 1;
for ($i = 0; $i < $firstSup; ++$i) {
for ($j = $i + 1; $j < $secondSup; ++$j) {
if ($numbers[$i] == $numbers[$j]) {
echo "{$i} and {$j} is the same : {$numbers[$i]}n";
}
}
}

<?php

/* $numbers is an array of number

* == Example

* $numbers = array(1,2,3,4,5,6,1,2,3,4,5,6,7,2,7,3);

$secondSup = count($numbers);

$firstSup = $secondSup - 1;

for ($i = 0; $i < $firstSup; ++$i) {

for ($j = $i + 1; $j < $secondSup; ++$j) {

if ($numbers[$i] == $numbers[$j]) {

echo "{$i} and {$j} is the same : {$numbers[$i]}n";

}

このアルゴリズムに含まれる if 文の時間計算量は ( O(1) ) です、 ( n ) に依存しませんから。 for 文の繰り返しは、外側が ( n-1 ) 回、内側が ( n – i ) 回です。よってこのアルゴリズムの時間計算量は ( O(n^2) ) 回です。

別の書き方をしてみます。 if 文の実行時間を ( c ) とします。すると、 for の繰り返しにより、全体の実行時間は

[ c sum_{i = 1}^{n – 1} {n – i} = frac{1}{2} c n (n – １) ]

となり、 ( O(n^2) ) であることがわかります。

もし for の中の $j < $secondSup や $j++ に時間がかかると考えても同じことです。 ( O(n^2) ) になります。

では次のアルゴリズムだとどうなるでしょうか。

asort($numbers);
$previousKey   = null;
$previousValue = null;
foreach ($numbers as $key => $value) {
if ($previousValue === $value) {
echo "{$previousKey} and {$key} is the same : {$value}n";
}
$previousKey   = $key;
$previousValue = $value;
}

asort($numbers);

$previousKey = null;

$previousValue = null;

foreach ($numbers as $key => $value) {

if ($previousValue === $value) {

echo "{$previousKey} and {$key} is the same : {$value}n";

}

$previousKey = $key;

$previousValue = $value;

}

PHP の組み込み関数で先に配列をソートし、隣り合う2つの要素の比較をしています。こうすることでループは1回で済みます。ただし、さきほどのスクリプトとは出力順序が異なります。

asort がどれくらい時間のかかる処理なのかわかりませんが、クイックソートだと仮定して、 ( O(n log_2 n) ) だとしましょう。すると、一重ループ ( O(n) ) に ( O(n log n ) ) が足されて、 ( O(n log n )) になります。

以上の評価から ( n ) が大きければ 2番目のコードのほうが速そうだといえます。ただ実際にやってみたところ、配列の要素が300件程度になったところで 10-20ミリ秒ほど2番目のコードの方が速くなりました。配列の要素が 20件程度だった場合は最初のコードのほうが速く終わりました。

今回の記事では、指標としてよく使われる計算量を取り上げましたが、よいアルゴリズムには読みやすさ、わかりやすさといった側面もあります。

The Life

アルゴリズムの評価

計算量

注意点

計算量の漸近的評価

オーダ記法 (O notation)

注意点

オーダの優劣

例

関連記事

この記事を見た人は次の記事も見ています

A Life Summary of an Gypsy