Table of Contents
シミュレーションはときに直感的な理解の助けとなります。 難しいことを理解するときには例を考えるのがいいのですが、手近に簡単なサンプルが見つからない場合は プログラムを使ってサンプルを作ってしまう、 シミュレーションをするのがおすすめです。
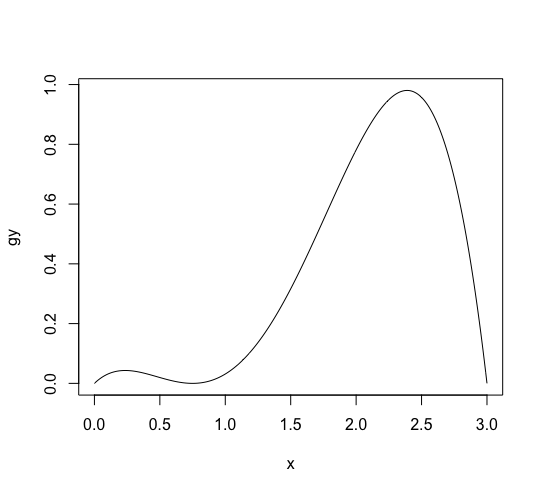
大数の法則についても、プログラムでシミュレーションができます。 たとえば (x in [0, 3)) を定義域で ([0, 1)) が値域の関数 ( g(x) = frac{1}{4} x(3-x)(x-0.75)^2) を考えてみましょう。 ((g(x)) は (int _0 ^1 g(x) dx neq 1) とならないので、 確率密度関数ではありません。 確率変数 (x) をプログラムでランダムに生成するために使う関数です。)
つぎの R のスクリプトで (g(x)) を描画できます。
|
1 2 3 4 |
g <- function(x) {x * (3 - x) * (x - 0.75) * (x - 0.75) / 4} x <- (0:300)/100 gy <- g(x) plot(x, gy, type='l') |
Suppose (x = 0, 0.01, 0.02, cdots , 2.99, 3), then P((x) = g(x) / (sum ^ {300} _ {k=0} g(100k) )).
|
1 2 3 4 5 |
s <- sum(gy) P <- function(x) { g(x) / s } y <- P(x) m <- sum(x * y) v <- sum((x - m) * (x - m) * y) |
ここで m は期待値、 v は分散で、 m が 2.16665 、 v が 0.2341004 です。
標本分布のテストをするために、次の関数を使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
pick <- function() { candidate = NA while (TRUE) { candidate = round(runif(1, 0, 3), 2) p = runif(1, 0, 1) if (p < g(candidate)) break } candidate } sample_average <- function(n) { v = 0 for (i in 1:n) { v = v + pick() } v / n } generate_distribution <- function(n) { r <- (0:300) * 0 for (i in 1:10000) { r[i] = sample_average(n) } table(r) / 10000 } |
それでは、 1標本、 2標本平均、 5標本平均、 50標本平均、 100標本平均 について分布をみてみましょう。
1標本
|
1 |
plot(generate_distribution(1)) |
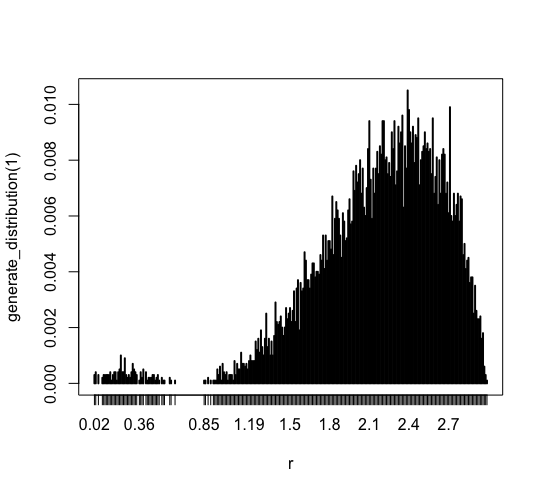
1標本の分布をテストしてみました。 これは確率関数 P に従った分布となります。
2標本平均
|
1 |
plot(generate_distribution(2)) |
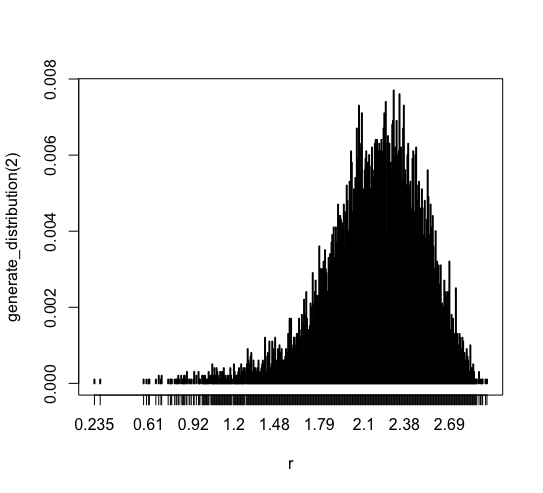
2標本平均の分布をテストしてみました。 1標本の場合と異なり、 ほとんどのデータは [1.79, 2.69] に集中しています。 そしてデータの範囲も1標本の場合よりも狭まっています。 0.2 より小さい値は無くなっていますね。
5標本平均
|
1 |
plot(generate_distribution(5)) |
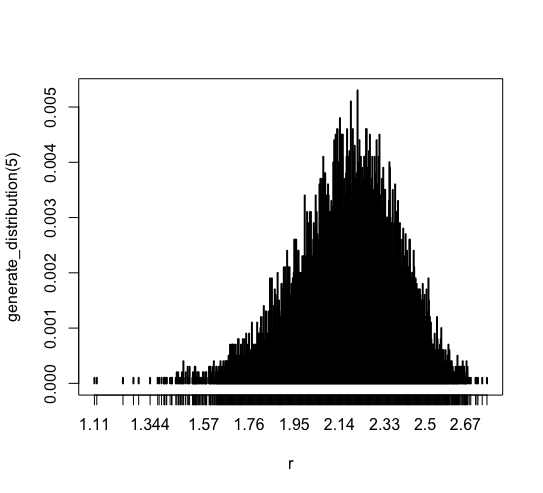
ほとんどのデータは [1.95, 2.5] に集中しています。 また、 最頻値は 期待値 2.16665 に近い値になっています。
50標本平均
|
1 |
plot(generate_distribution(50)) |
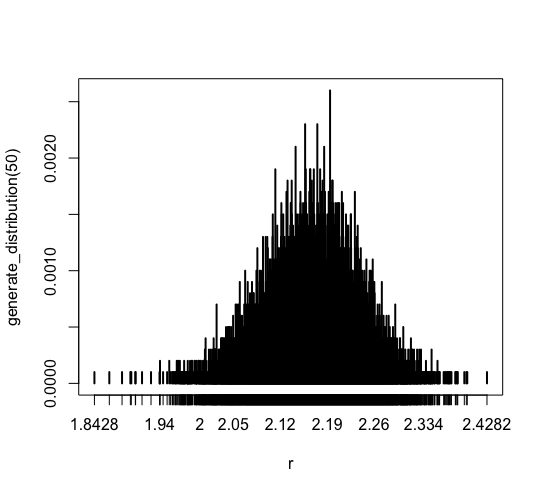
ほとんどのデータは [2.05, 2.26] に集中しています。
100標本平均
|
1 |
plot(generate_distribution(100)) |
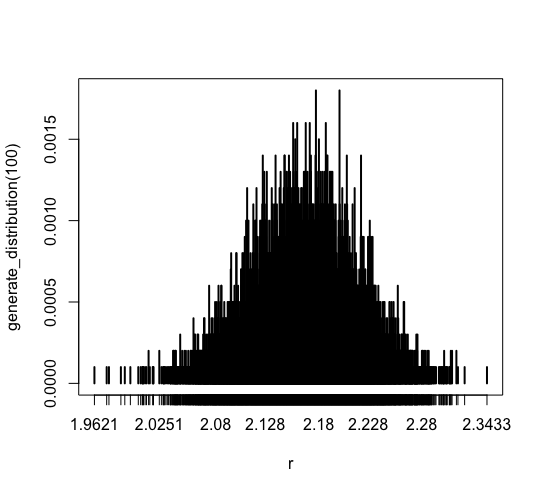
ほとんどのデータが [2.08, 2.228] に集中しています。 そして 1.9621 以下 や 2.3433 以上 のデータは出現していません。
この記事が大数の法則の理解の助けになれば幸いです。