Table of Contents
中心極限定理と大数の法則について、サンプルを見て理解を深めましょう。 シミュレーション手順を先に掲載しますが、難しければその部分を飛ばして最後の2つの図をご覧ください。
大数の法則と中心極限定理、およびそれらのシミュレーション結果を掲載します。
大数の法則
標本の数が大きくなれば、標本分布の標本平均は期待値周辺に集中する。
細かいことをいうと、大数の弱法則と強法則があり、次のように表現されます。
弱法則
(X_1, cdots , X_n) 全てが平均を (mu) とする同一の確率分布に従い、 それぞれ独立であるとき ( Y_n = frac{1}{n} sum _{k = 1}^n X_k) について (forall varepsilon , textrm{P}(|Y_n -mu| gt varepsilon ) rightarrow 0 textrm{as} n rightarrow infty )。
強法則
(X_1, cdots , X_n) 全てが平均を (mu) とする同一の確率分布に従い、 それぞれ独立であるとき ( Y_n = frac{1}{n} sum _{k = 1}^n X_k) について ( Y_n rightarrow mu textrm{as} n rightarrow infty ).
中心極限定理
任意の確率分布について、標準化された標本平均の分布は、標本数を増やすと標準正規分布に収束する。
これは、標本平均の分布が正規分布に収束すると表現しても意味は同じです。
標準正規分布
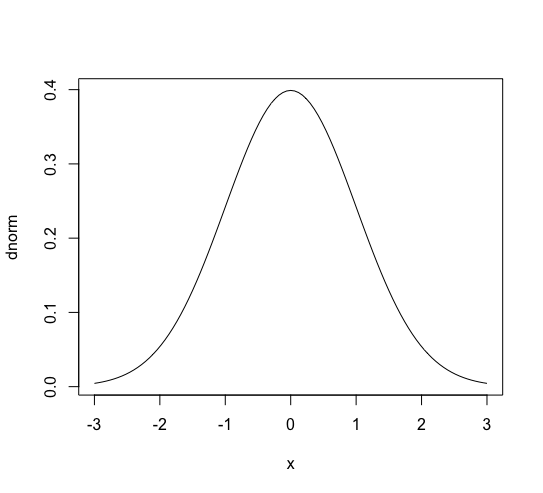
標準正規分布は確率密度関数 (f(x) = frac{1}{sqrt{2 pi} } exp left( – frac{x^2}{2}right)) で表される、 期待値 0, 標準偏差・分散 1 の分布です。
( -3 leq x leq 3 ) については R で plot(dnorm, xlim=c(-3, 3)) を実行するとグラフが表示されます。
標準化
確率変数 (x) の 期待値を (mu), 標準偏差を (sigma) としたとき、 (x) から (frac{x-mu}{sigma}) に変換することを標準化といいます。 変換後の (frac{x-mu}{sigma}) は 期待値が 0, 標準偏差および分散が 1 になります。
シミュレーション
これらを視覚的に理解するためにシミュレーションを行います。
一様分布などでシミュレーションをしても面白みがないので、 ( x in [0, 3] ) について次の関数を使って確率分布を作ります。
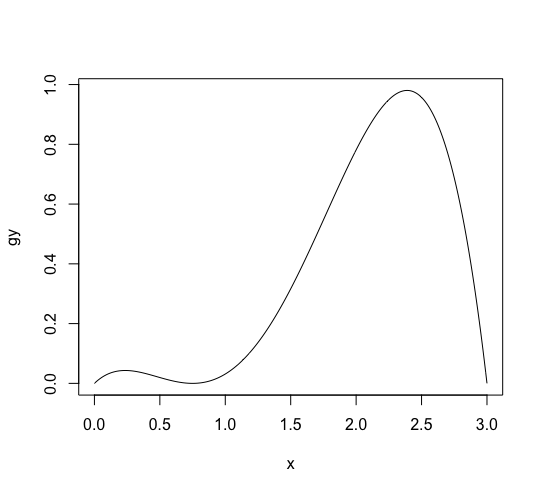
[g(x) = frac{1}{10} (3-x)(x-0.4)^2 (x+1) + 0.05 ]この関数のグラフは次のコマンドで表示できます。
|
1 2 3 4 |
g <- function(x) {((3 - x)*(x - 0.4)^2 *(x + 1) + 0.5)/10} x <- (0:300)/100 gy <- g(x) plot(x, gy, type='l') |
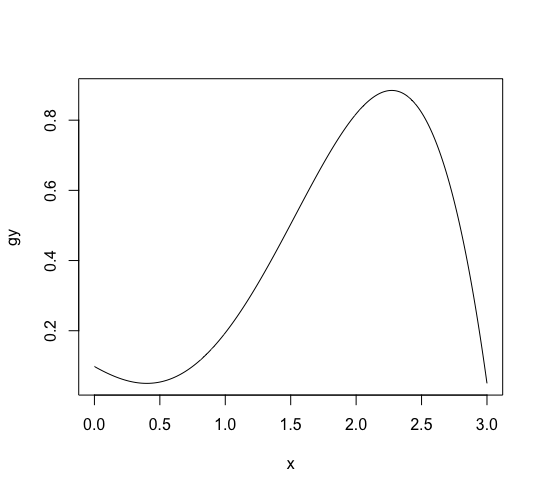
これは確率密度関数ではないことに注意してください。 (g(x)) は確率変数のシミュレーションするための関数で、 (x in [-3, 3] ) で 0以上1以下の値をとります。 これを利用して ([0, 1)) の乱数から確率変数の分布を作ります。
実際には (x = 0, 0.01, 0.02, cdots , 2.99, 3) として、 その確率は (textrm{P}(x) = g(x) / left( sum _{300}^{k=0} g(k/100) right) ) となります。 これは次の R のコマンドでその折れ線グラフを表示できます。
|
1 2 3 4 5 |
s <- sum(gy) P <- function(x) { g(x) / s } y <- P(x) m <- sum(x * y) v <- sum((x - m) * (x - m) * y) |
ここでの R のオブジェクトは次のようになっています。
gy |
(g) による (x) の計算値。 |
P |
(x) の確率関数。 |
y |
x に対応する確率で、 P で計算された値。 |
m |
期待値。 1.97606。 |
v |
分散。 0.3572804。 |
先ほどは (g(x)) のグラフを表示しましたが、 実際の (x) の確率 (textrm{P}(x)) を表示するには plot(x, y * 100, type='l') を実行します。
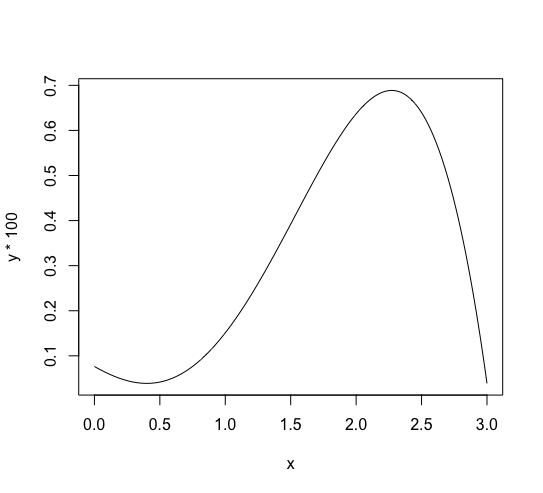
シミュレーションを行うため、次のオブジェクトを用意しておきます。
pick |
(x) をひとつランダムに出力する関数。 |
sample_average |
標本平均を計算する関数。 |
generate_distribution |
標本を N に格納された数だけランダムに作る関数。 引数は標本平均を作るときの標本数を表す。 |
draw_original |
標準化されていない (x) のヒストグラムを折れ線で描く関数。 グラフに表示するため、四捨五入を行うなどの補正を行なっている。 |
draw |
標準化された (x) の確率分布を折れ線で描く関数。 グラフに表示するため、四捨五入を行うなどの補正を行なっている。 |
N |
シミュレーションで使用する標本の数。 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
N = 100000 pick <- function() { candidate = NA while (TRUE) { candidate = runif(1, 0, 3) p = runif(1, 0, 1) if (p < g(candidate)) break } candidate } sample_average <- function(n) { c = 0 for (i in 1:n) { c = c + pick() } c / n } generate_distribution <- function(n) { r <- (0:300) * 0 for (i in 1:N) { r[i] = sample_average(n) } r } draw_original <- function(n) { X = generate_distribution(n) plot( table(round(X, 2)), xlim=c(0, 3), ylim=c(0, 6000), type='l', col=rgb(1/n, 0, 1-1/n), xlab="", ann=FALSE, axes=FALSE ) } draw <- function(n) { X = generate_distribution(n) plot( table(round((X - m) / sqrt(v/n), 1)) * 10 / N, type='l', xlim=c(-3, 3), ylim=c(0, 0.4), col=rgb(1/n, 0, 1-1/n), xlab="", ann=FALSE, axes=FALSE ) } |
大数の法則
大数の法則をシミュレートします。 次のコードで、 単純な標本についてのヒストグラム、 4つの標本についてのヒストグラム、 100標本についてのヒストグラムを表示できます。
|
1 2 3 4 5 6 7 |
draw_original(1) par(new=T) draw_original(4) par(new=T) draw_original(100) axis(side=1, at=0:3) axis(side=2, at=(0:6) * 1000) |
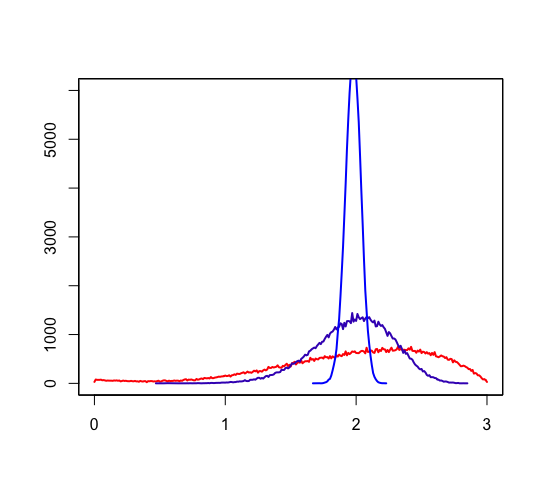
赤色が標本のヒストグラム、紫色が4標本の平均のヒストグラム、青色が100標本の平均のヒストグラムです。
期待値 1.97606 に分布が集まっていくのがわかりますね。
中心極限定理
中心極限定理をシミュレートします。 次のコードで、 単純な標本についての確率分布、 4つの標本についての確率分布、 100標本についての確率分布を表示できます。
|
1 2 3 4 5 6 7 |
plot(dnorm, xlim=c(-3, 3), ylim=c(0, 0.4)) par(new=T) draw(1) par(new=T) draw(4) par(new=T) draw(100) |
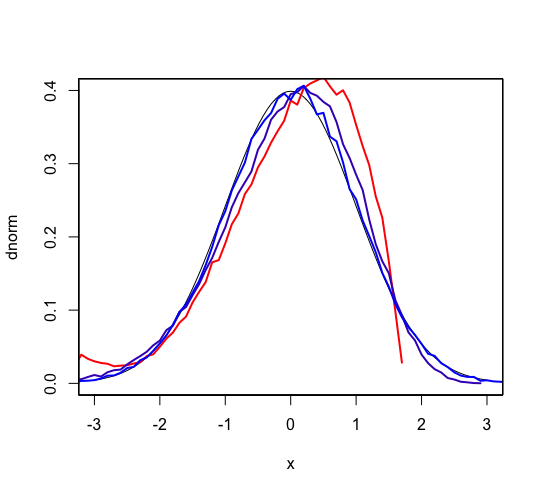
黒い線が標準正規分布、 赤色が標本の分布、紫色が4標本の平均の分布、青色が100標本の平均の分布です。 1標本では2以上の値が分布に現れませんが、 100標本の平均では3を超える値も出てきていて、 正規分布にそっくりになっていますね。