Table of Contents
幾何分布と負の2項分布について例を紹介します。
例題
2つのサイコロを同時に振ります。 この試行をAと呼ぶことにします。 両方とも1が出る場合を T, そうでない場合を F と表現することにします。
試行AをTが出現するまで繰り返し、 Tが出た時点で終了とします。 この試行をBと呼ぶことにします。
試行Bにおける、Fの回数、すなわち サイコロを振った回数から1引いたものを R と呼ぶことにします。 サイコロを振ったけれども両方とも1にならなかった回数です。
試行Bを cc 回 繰り返したときの、 R の平均を XX とします。
XX の確率
c,Xc,X についての確率を P(c,X)P(c,X) と書くことにします。
(c=1) の場合を考えます。 基本的に サイコロを1回振るとき、 T の出る確率は 136136 、 F の出る確率は 35363536 です。 P(1,X)P(1,X) は F が XX 回続いた後で、 T が出る確率ですから、
P(1,X)=(3536)X136P(1,X)=(3536)X136となります。 これはX(=cX)X(=cX)についての幾何分布です。
一般の cc について考えます。 サイコロを 全部でサイコロを振るのは (cX+c)(cX+c) 回 です。 このような目の出方になるのは、 cc回の T のいずれかの前に、 cXcX回のFを並べる重複組み合わせ XHcX(=c+cX−1CcX=c+cX−1Cc−1)XHcX(=c+cX−1CcX=c+cX−1Cc−1)です。 見方を変えると、 最後のゾロ目を除いた (c+cX−1)(c+cX−1)回の中でどの(c−1)(c−1)回を T にするかの組み合わせ c+cX−1Cc−1c+cX−1Cc−1 です。 c>1c>1 では XX は整数以外の値をとることに注意してください。
その確率は、
P(c,X)=c+cX−1Cc−1(3536)cX(136)cP(c,X)=c+cX−1Cc−1(3536)cX(136)cとなります。 これは cXcX についての 負の二項分布です。 XX については複数回の試行BBでの平均の分布ですから、中心極限定理が成立します。
確率分布をグラフにする
c=1,2,5,10,20,50,100c=1,2,5,10,20,50,100 の場合の折れ線グラフを表示してみましょう。 Excel や LibreOffice では、 COMBIN 関数 で組み合わせを計算できますので、 それを利用してグラフを描画します。
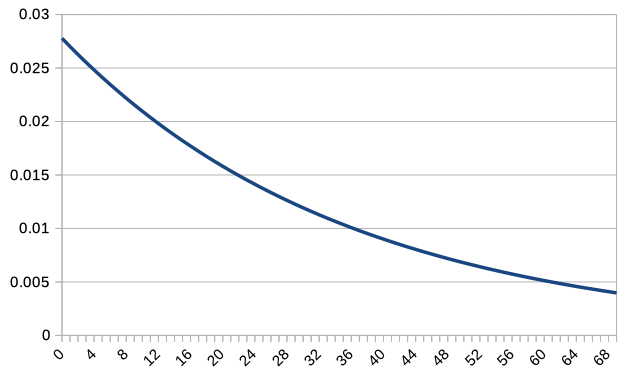
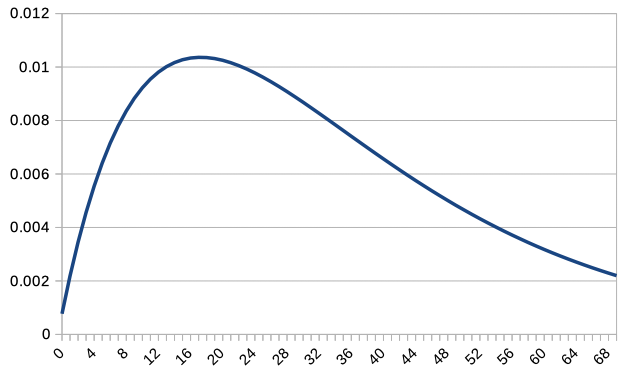
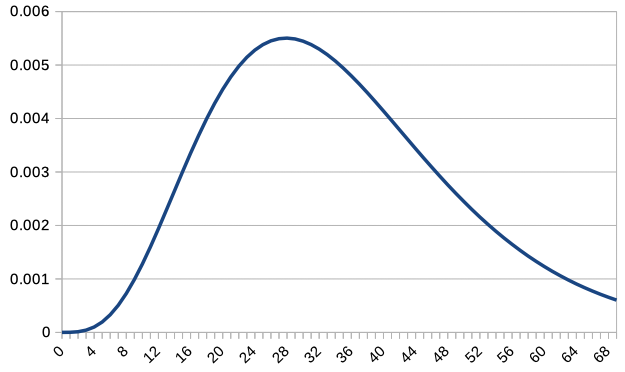
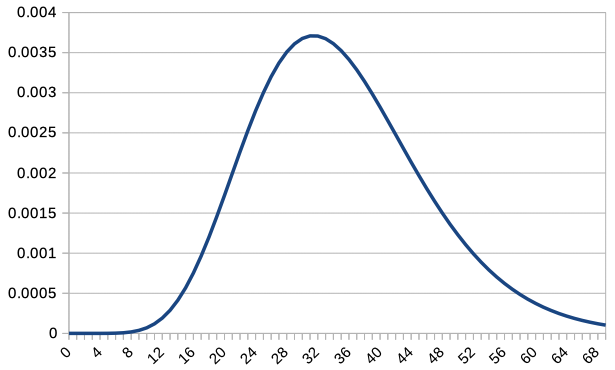
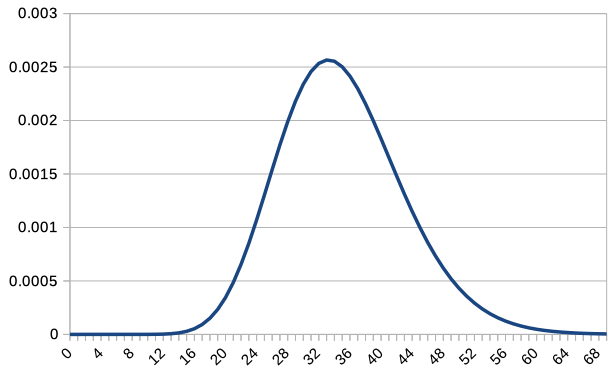
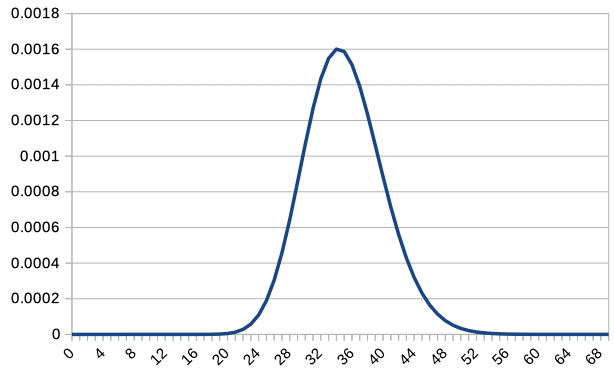
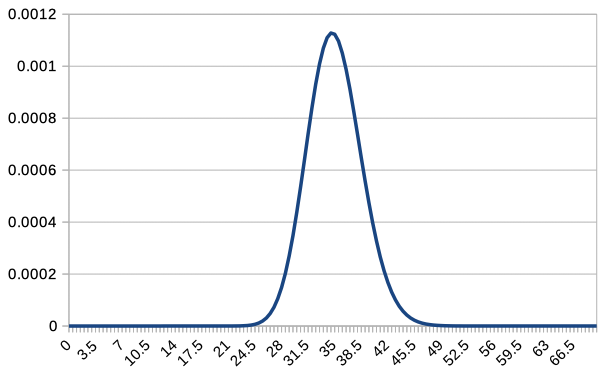
全部を一緒に重ねるとみづらくなってしまうので、 cP(c,X)cP(c,X) のグラフを c=1,2,5,10,20,50,100c=1,2,5,10,20,50,100 について重ねて表示します。 整数値の X についてしかプロットしていませんので、 c=100 のグラフは少し粗くなっています。
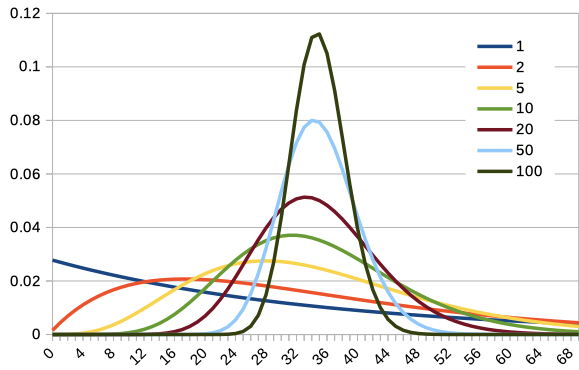
c=1 では左右非対称どころか右肩下がりの分布でしたが。 c を増加させることで正規分布に似てきていますね。 c を増加させると X=35 が一番確率の大きくなる値になるように、分布が変化していきます。
幾何分布
c=1 の時は幾何分布でした。 幾何分布が X=1,2,3,⋯ について P(X)=p(1−p)X−1 で表される時、 E(X)=1p, V(X)=1−pp2 です。
上の例では p=136 として P(X)=(1−p)⋅p(1−p)X と書けるので、 期待値は E(X)=1−pp=35 、 分散は V(X)=35⋅36 となります。
負の2項分布
c=1 も含めて 一般の c では負の二項分布でした。 負の二項分布は k 回目 の成功を得るまでの失敗回数 X(=0,1,⋯) についての確率が P(X)=k+X−1CXpk(1−p)X で表される時、 E(X)=k1−pp, V(X)=kqp2 となります。
上の例では p=136, c 回目 の成功を得るまでの失敗回数 cX についての負の2項分布として P(cX)=c+cX−1CcXpc(1−p)cX と書けるので、 E(cX)=c35, V(cX)=c35⋅36 となります。 これより E(X)=35, V(X)=35⋅36c です。 確かにグラフで見たのと同じように、期待値は 35 になります。
