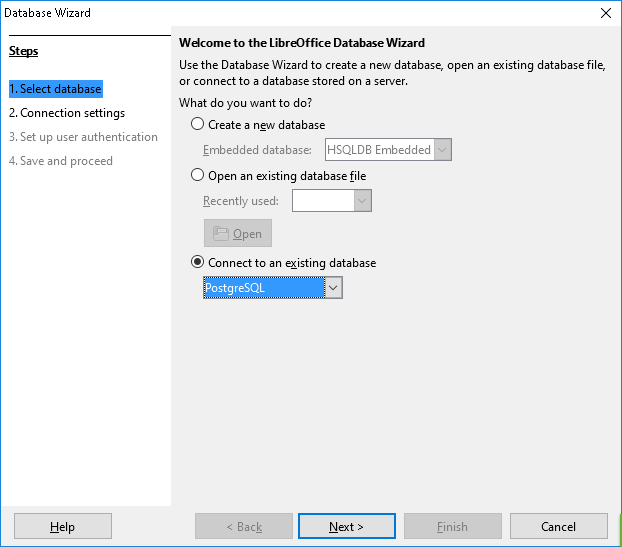
無料で使える表計算ソフト LibreOffice Calc の Basic でセルを扱う方法を説明します。 Excel VBA だと Cell(1, 2) のように扱えますね。
「公式」タグアーカイブ
数学: 球の体積を導出する
円の面積を導出する に続いて 球の体積 ( ( frac{4}{3} pi r ^3 ) ) を導出してみることにしました。 半径1の球について考えます。
続きを読む 数学: 球の体積を導出する数学: 円の面積を導出する
円の面積がなぜ \( \pi r^2 \) ( \( r \) は半径 ) になるのかを説明します。 (使っている図が悪いので後日差し替えます。)
掛け算で三角形の面積を求めるものの、その他の積分計算や極限計算は使わないようにしました。 掛け算の記号 ( \( \times \) ) を省略することと、 文字で数を表していることと、 \( x ^2 = x \times x \) と、 ルート ( \( \sqrt{x} \) は \( \sqrt{x} \times \sqrt{x} = x \) となる正の数 ) がわかれば中学校あるいは小学校の算数・数学で理解できると思います。
続きを読む 数学: 円の面積を導出する\( k^n \) の総和 公式の導出
1から100まで足すといくらになるか。
ガウスがこの計算を即座にやってのけたという話はあまりに有名で、整数を順次足す、等差数列を順次足す方法はご存じの方も多いと思います。
よく使われる説明の方法として、石を三角の形に置き、それと点対象な三角の形に石を置くというのがあります。
続きを読む \( k^n \) の総和 公式の導出オイラーの多面体定理を証明する
オイラーの多面体定理を考えてみましょう。 (もともとはグラフ理論での定理なのですが。)
オイラーの多面体定理
多面体では次の等式が成り立つ。
頂点の数 – 辺の数 + 面の数 = 2
平面上の図形においてもこの式は成り立つ。
今回はこの式が本当に正しいのか検証してみようという趣旨です。 オイラーの式は平面上で成り立つ式なので、平面上で考えます。 多面体は平面図形に置き換えられるので、 平面図形でオイラーの式が成り立てば 多面体でも成り立つことになります。
多面体を平面に投影する
多面体は平面図形に投影することができます。
左の4面体は右のように平面に投影できます。 4面体の面は4角形になったのが3つ、残る面はまわりのエリアです。 点と線で 4つの区域に分けられていますね。
証明
平面上に描かれた点と線を考えます。 線の両端が点だと考えてください。 全ての線は点を介してつながっているものとし、点以外では線がつながらないものとします。 線は曲線も含みます。
数学的帰納法で考えます。 点の数を \( V \) 、 線の数を \( E \) 、 面の数を \( F \) とします。 \( V – E + F = 2 \) を証明すればOKです。
\( E = 1 \) のとき
辺 \( E \) は 1, 面 \( F \) は 1, 点 \( V \) は 2 です。
\[ V – E + F = 2 – 1 + 1 = 2 \]オイラーの式は成立しています。
\( E = k \in \mathbb{N} \) でオイラーの式が成り立つとき
\( E = k \) でオイラーの式が成立するときの \( E \) 、 \( V \) 、 \( F \) の値をそれぞれ \( E_k \) 、 \( V_k \) 、 \( F_k \) とすると、次の式が成り立ちます。
\[ V_k – E_k + F_k = 2 \]ここで \( V_k \) 、 \( F_k \) の値は \( k \) によって一意に定まるものではなく、 あくまで前提とした条件での値です。
図形に線を足す場合を考えます。 線は点を介してつながっているので、新しく引く線は両端または一方の端が既存の線とつながります。
線の一方のみが既存の点に接続する場合
点が新たに1つ増えるので \( V = V_k + 1 \) 、 線が新たに1つ増えるので \( E = E_k + 1 \) 、 面の数は変わらないので \( F = F_k \) 。
\begin{array}{cl} & V – E + F \\ = & ( V_k + 1 ) – ( E_k + 1 ) + F_k \\ = & V_k – E_k + F_k \\ = & 2 \end{array}線の両端が既存の点に接続する場合
新しく線を引く前の状態で、 既存の線は繋がっているため 新しく引く線の片側または両側は線が閉じていることになる。 すなわち線を新しく引くと、 面の数が1増える。
これより 点の数は増えず \( V = V_k \) 、 線の数は1増えて \( E = E_k + 1 \) 、 面の数も1増えて \( F = F_k + 1 \) 。 これは 線の始点と終点が同じ場合も含みます。
\begin{array}{cl} & V – E + F \\ = & V_k – ( E_k + 1 ) + ( F_k + 1 ) \\ = & V_k – E_k + F_k \\ = & 2 \end{array}以上より、 \( E = k \in \mathbb{N}\) で オイラーの式が成立していれば \( E = k + 1 \) でも成立することが分かる。
よって すべての場合で オイラーの式は成立する。
証明にしてはちょっとゆるい感じがしますが、 式が成り立つことを理解していただけるとうれしいです。
このオイラーの定理を使うと、デカルトの定理も証明できます。 詳細は デカルトの定理を証明する をご覧ください。